Video Game Dialogues and Graph Theory

How Talking Works

In video games with interactable characters the player often communicates with them via dialogue. This is almost always represented in the following fashion:

• A text prompt is given, usually the speech of a character
• The player is given options to answer
• Choosing an option triggers a new prompt and the cycle repeats

This basic framework is sufficient to simulate some kind of social interaction within games. Some dialogue-heavy games like Planescape Torment only feature few other mechanics aside from it and Disco Elysium features nothing but this simple system for the player to interact with NPCs. This kind of dialogue is a staple of the role-playing genre.

This system is often referred to as a dialogue tree, but I believe this term to be highly deceptive. I see them more as a dialogue graph. In this section I want to explore the different kinds of graphs game designers can use when writing their dialogue.

In the following, different dialogue systems are visualized by circles denoting prompts and arrows denoting player choices.

The Unique Paths

The easiest structure to imagine in a dialogue is also one that is rarely used.¹ Every choice the player makes, causes the dialogue to span into new unique options, which in turn lead to completely new prompts and options. Therefore, every path through the dialogue is completely unique.

While this might be cool to build into a game an obvious problem is the number of unique prompts and options one would need to write. For the sake of argument let us assume that the number of choices for each prompt is the same over the whole conversation. Then the number of prompts for a specified number of choices c for any depth of the conversation d (the number of choices made before the conversation ends) is d multiplied with itself c times. The sums of these products is the total number of prompts.

$$ P(c, d) = \sum_{i=0}^d c^i $$

The total number of choices can be computed based on this measure, as each prompt, except for the prompts at the very end (the depth of d) leads to c choices to make.

$$ C(c, d) = P(c, d-1) * c $$

The amount of text segments that would need to be written for a single conversation is then the sum of those two functions.

$$ A(c,d) = P(c,d) + C(c,d) $$

When there are three distinct choices for each prompt and the conversation goes on for five choices made, this translates to 727 text segments that have to be written. Take the depth to six and the number jumps up to 2.185. Keep the depth at five and bump the number of choices to five the final result is 7.811. Bump the depth to ten and you will end up with 24.414.061 texts!²

This combinatorial explosion is a clear reason why this kind of dialogue graph is not being used often as it requires writers to produce a very large number of prompts, which quickly becomes so big that it would be humanly impossible to write them all.

The Pseudo-Choice

The most disappointing kind of dialogue graph is the pseudo-choice. The player is given choices that ultimately do not matter. After the choice has been made, different prompts are triggered which are then resolved to the same prompt. The next choice behaves completely independent of the choice made before and therefore wasn’t an impactful choice after all.

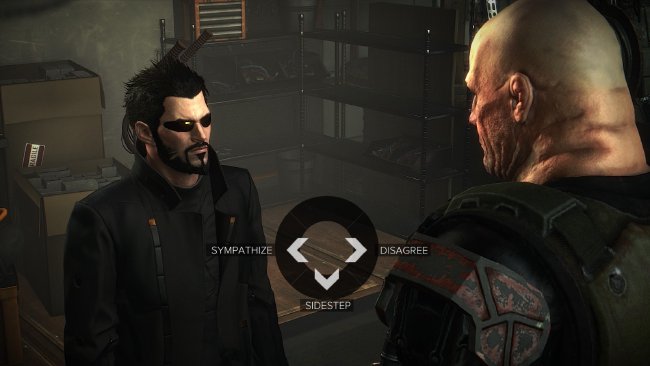
While the choices trigger unique prompts, the conversation itself is not unique and has no dynamic direction. In Deus Ex: Mankind Divided the first conversation with Marchenko serves as an example.

This kind of dialogue is a simple way of dealing with the combinatorial explosion that occurs when branching to much. I personally find it tiring since it fundamentally defeats the purpose of having any choice. If the choice never mattered why even have it in the game?

The Question Loop

Sometimes dialogue is used as a tool for exposition. An interactive way of doing so is the player gaining information from a character in the game via repeatedly asking questions. In dialogue form, a prompt is followed by multiple choices, most of which trigger a prompt which then resolves to the original prompt, looping the conversation and giving the player the chance to continue with another (or the same) choice.

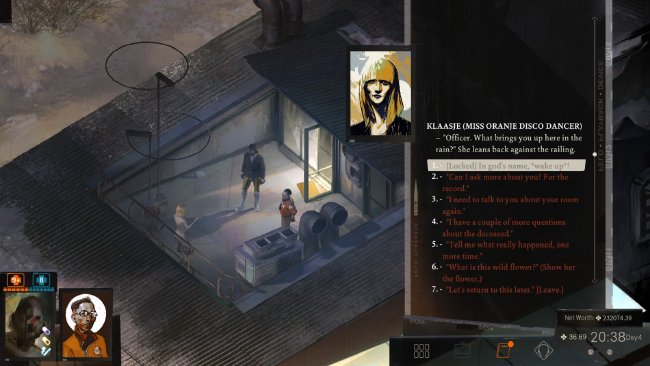
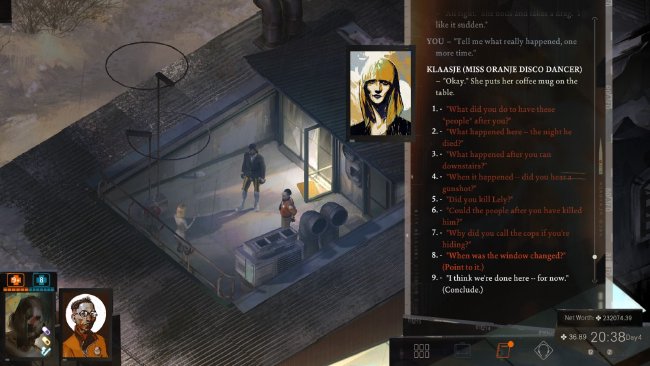
This is frequently used in Disco Elysium and fits in perfectly into its detective gameplay, since asking questions is what a detective does. It serves as a way of dumping exposition while still giving the player a way of interacting with the story.

However, a consequence of this design is that questions can be infinitely retried, which spawns the same prompts every time. This gives the player the chance to reread answers, but obviously isn’t natural and can break immersion.

The Check

Role-playing games are almost synonymous with speech-checks in their dialogues. When the checks are visible, certain choices become available based on attributes of the player’s character, such as a speech skill.

Thus, the dialogue itself is static, but changes shape based on the player’s choices. The experience is personalized to the player’s character and gives more depth to its creation.

These checks can use absolute values (Speech > 70, Reputation > 50, etc.) or random dice throws in conjunction with these values to determine wether a check succeeds or not. With hidden checks, the dialogue feels more lively, the outcome is less predictable and arguably more fun.

This system is so common, that it would make no sense to name single examples. You can find a list of some games that use it here.

The Back Button

In order to let the player take more direct control over the conversation the developer can introduce a two-way option that allows to rewind and go back to the previous option. Therefore the dialogue becomes a menu that uses its choices to go into sub-menus and back again. This is helpful for having structured questioning or letting the player change topics dynamically.

However, similar to loops in dialogue, it feels extremely strange being able to go back and forth indefinitely within a dialogue. I also assume that giving players the ability to rewind will let them read the text less carefully since they can always simply go back to what they read before.

Environment Aware Dialogues

Lately I am interested in designing dialogues that are more natural, dynamic and put more weight into player choices. My idea is a dialogue system that imposes restrictions on the designer to limit themselves to dialogues that explicitly disallow loops. This gives rise to possibilities of giving player choices side-effects which can safely be implemented.

Directed Acyclic Graphs

So far, we have analyzed different configurations of prompts and choices as graphs. Graph theory is a discipline in mathematics that is all about studying these structures. While we will not go into depth on this subject here we still want to use some of graph theories results in building a dialogue system.

Graphs generally consist of nodes and edges. Edges are connections between nodes. They can be directed, meaning that they have a direction, or undirected. Dialogues generally are directed graphs, since a choice (an edge in a graph) is a connection from one prompt (node in a graph) to another in only one direction.

As we have already discussed, loops in dialogues diminish player choice and immersion. Therefore loops should be abolished from the new system. This will make the dialogue turn into a directed acyclic graph (DAG). In general this means that the graph is directed (duh!) and does not contain loops.

However, this does not mean that the graph is a tree, since trees need to have unique paths between any two nodes. This simple graph serves as a counterexample:

Reaching the last node from the first has three distinct paths. However, it is possible for DAGs to have trees as their underlying structure. If that is the case, the structure becomes a polytree (also called a directed tree).

As we can see in this graph, there are no loops and each path between two nodes are always unique. However, there can be multiple starting points which then resolve to the same nodes. To me this is a very natural way of modeling dialogues. In conversations we usually don’t provide a question and answer session where we repeat the same answers over and over again, and things that are said always have some impact on what will be said next. Conversations are interactions after all. This model therefore rules out the pseudo-choice, question loop and back button in dialogues.

Properties of Directed Acyclic Graphs

DAGs are interesting from a technical point of view. On them we can define a topological sorting, which is a fancy term for an ordering of the nodes of the graph. This can help us to automatically order and create IDs for nodes in a dialogue, which could aid in designing a dialogue system that facilitates internationalization out of the box!

Another great property of DAGs is that since we cannot loop or go back in the graph, each edge (in our case dialogue choice) can only be taken once! This is helpful, when trying to interact with an environment.

Connecting Environments to Choice

I would love for dialogue choices to have a real impact on the characters and world around the player. For example, if I, the player, tell a character about some fact I know, I would expect the character to remember that I have told them about said fact. Also, when I am friendly to a character I would hope them to change their behavior in later conversations.

This can be modeled as side-effects inside our dialogue graphs. Each choice writes to a global environment. Here we see a simple example with a good and bad choice:

Why is this helpful? As we have discussed, we can perform visible and invisible checks inside dialogue, which can then again read from the modified environment.

If you start with a sentiment of 60, you can still make the “bad” choice and go into the yes branch. Here we see, why it is very important for our graphs to be acyclic. If we had any loops, we would be able to perform the same side-effects multiple times! Using DAGs as our underlying structure, we do not have to perform any additional checks when applying side-effects, as we know that each choice can only be made once.

I hope that this will lead to a new way of writing video game dialogues where choices are much more impactful. Each choice a player makes should feel final. The world has to react to things said and the player should be made to react to the world.

Conclusion

As we have explored, different types of dialogues in video games exist and most of them are not suitable to facilitate realistic conversations. I believe using DAGs and polytrees as the underlying structure for such dialogue will give rise to a new way of writing them, since interactions with the environment become easier to reason about. Therefore, writers can put more emphasize in writing choices that impact the outcome of later conversations in a more meaningful way.

At least that’s my theory. I will invest some time into the investigation whether this actually works. If I find anything interesting I will probably write a post about it.